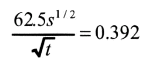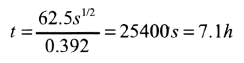Diffusion Through a Packaging: Polymer Permeability
A polyethylene filme 0.00015 m (0.15mm) thick is being considered for use in packaging a pharmaceutical product at 30 degrees Celsius. If the partial pressure of Oxygen outside is 0.21 atm and inside the package it is 0.01 atm, calculate the diffusion of Oxygen at steady state. Use permeability data from Table 6.5-1. Assume that the resistances to diffusion outside the film and inside are negligible compared to the resistance of the film.
Solution:
From Table 6.5-1
PM = 4.17(10-12) m^3 solute (STP) / (s*m^2*atm/m).
Substituting into,
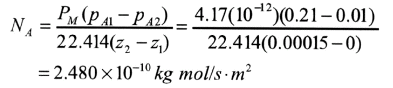
Note that a film made of Nylon has a much smaller value of permeability, PM for Oxygen and would make a more suitable barrier.
All equations and tables were taken from, Geankolis, Christie J., Transport Processes and Unit Operations, Newton Massachusetts, Allyn and Bacon Inc., 1983
Diffusion of Boron into a Silicon Wafer: Electronic Materials
Boron is predeposited on a silicon wafer with an initial concentration of 5 x 1015 atoms cm-3. Conditions are 30 minutes at 1223 K. Calculate a) the amount deposited; b) the diffusion length; c) the concentration at the diffusion length.
Solution:
a) From Table 6.5-1,
Cs - 4.5 x 1020 atoms cm-3 and
The equation
b) Equation (13.51)
Notice how small l is, this is typical.
c) Equation (13.47) applies with
thus with Table 5.1 we get
All equations and tables were taken from, Poirier, D. R. and G.H. Geiger, Transport Phenomena in Materials Processing, TMS, Warrendale, Pennsylvania, 1994.
Diffusion of Carbon into Iron:
For some applications, it is necessary to harden the surface of a steel (or iron-carbon alloy) bove that of its interior. One way this may be accomplished is by increasing the surface concentration of carbon in a process termed carburizing; the steel piece is exposed, at an elevated temperature, to an atomsphere rich in a hydrocarbon gas, such as methane (CH4).
Consider one such alloy that initially has a uniform carbon concentration of 0.25 wt% and is to be treated at 950 degrees Celsius (1750oF). If the concentration of carbon at the surface is suddenly brought to and mainted at 1.20 wt%, how long will it take to achieve a carbon content of 0.80 wt% at a position 0.5 mm below the surface? The diffusion coefficient for carbon in iron at this temperature is 1.6 x 10-11 m^2/s; assume that the steel piece is semi-infinite.
Solution:
Since this is a nonsteady-state diffusion problem in which the surface composition is held constant, Equation 5.5 is used. Values for all paramters in this expression except time t are specified in the problem as follows
Co = 0.25 wt% C
We must now determine from Table 5.1 the value of N for which the error function is 0.4210. An interpolation is necessary, as
Therefore,
and solving for t,
To see how this solution is related to diffusion in two dimensions play, the following two animations where carbon is exposed over a small and large surface area. In both animations the student can observe how the two-dimensional ( numerical ) solution converges to the exact one dimension steady steady state ( analytical ) solution, shown as a dashed line.
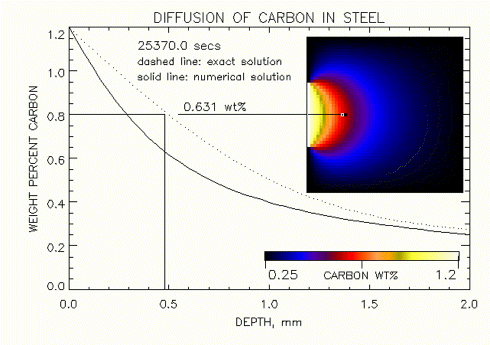
Figure 1. Comparision of 1-D (analytic) and 2-D (numeric) solutions of carbon diffusing into Iron, at "steady state" ( time -> 25,400 sec ), where carbon is exposed only over a small surface area.
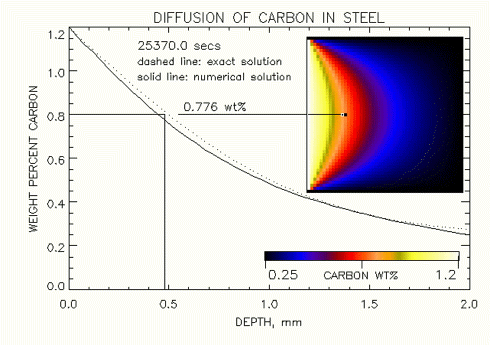
Note that the boundary conditions have a very large influence on the gradient in concetration of carbon that diffusses into the iron along a one dimensional line as show in the two figures shown below at the steady state condition. Figure 1. shows that a low concentration of carbon is predicted by the numerical solution when a smaller area of the Iron is exposed to carbon at 1.2 wt% at 0.5mm below the surface. In Fig. 2 at this same point we can see that this concentration of carbon increases when a large area of the surface of iron is exposed to carbon. In fact in the limit, as the entire surface or the iron is exposed to carbon, we will observe that the concetration of carbon at 0.5mm approaches the exact steady state solution result of 0.8 wt%.
Figure 2. Comparision of 1-D (analytic) and 2-D (numeric) solutions of carbon diffusing into Iron, at "steady state" ( time -> 25,400 sec ), where carbon is exposed over a larger surface area.
To see how these animations were made go to the section on Scientifc Visualization. To see how the numeical solution is obtained go to the Numerical Methods section of this class project.
End of example problems by Roxanne Cox
D= 1.6 x 10-3 micron m^2 / h.
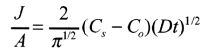applies, so that
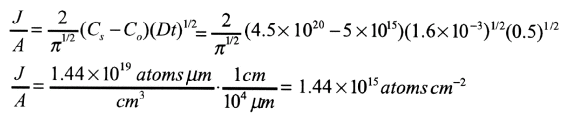
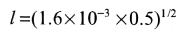is used.
,
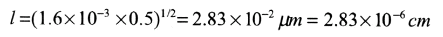
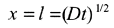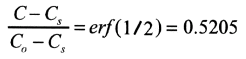and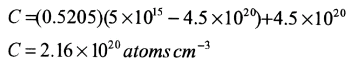
Example Problem 5.2 of class textbook, pg 97 of "Materials Science and Engineering: An Introduction" by W.D. Callister, Jr.
Cs = 1.20 wt% C
Cx = 0.80 wt% C
x = 0.50 mm = 5 x 10-4 m
D = 1.6 x 10-11 m2/s
Thus,
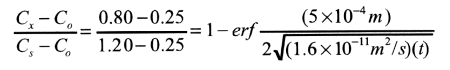
z erf(z )
0.35 0.3794
z 0.4210
0.40 0.4284
N = 0.392
