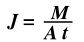
by John Stuecker (resume). Modified by R.D. Kriz (5/18/95).
Diffusion is the phenomenon of material transport by atomic motion. For example, if there are metals joined together so contact is made, diffusion will occur. The rate at which this occurs is dependent on temperature. The higher the temperatures of the two metals, the faster diffusion will occur. If the two metals joined together are the same, self diffusion occurs. If the two neighboring metals are different interdiffusion will occur. In both instances, the net drift of atoms will happen form higher to lower concentration regions.
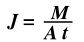
When two species diffuse into each other, it is necessary to know the rate of mass transfer. This is known as diffusion flux which is defined by the above equation. When differentiated to take the rate of diffusion into account, this equation becomes.
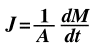
If the diffusion flux (J) does not change with time, then we have reached a condition of steady state diffusion. In other words, steady state is reached when the amount of atoms diffusing through an area does not change as time changes. To explain this phenomenon further, recognize gas particles diffusing through a metal plate. If the concentrations of gas molecules are held constant on both sides of the plate then it is said that steady state is reached. It can also be recognized that the flux (J) is proportional to the concentration gradient (delta C/delta X). This relationship at steady state is known as Fick's First Law, developed by Adolf Fick.
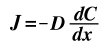
If the conditions dictate that a steady state is not occurring, Fick's First Law can no longer be used and the concentration is differentiated with respect to time to give the equation known as Fick's Second Law where the gradient of contentration with respect to time is equal to the gradient of the flux, J, with respect to postion, x, which is the same as the double derivative of concentration with respect to position, x. This assumes of course that the diffusion coefficient is not a function of position. Other assumptions are listed below.
Assumptions made to solve this equation for a given example are necessary.
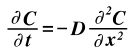
When these boundary conditions are applied, the resulting solution is:
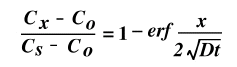
An ANALYTIC SOLUTION of Carbon diffusing into Iron based on the concepts above.