Transient Behaviour
In order to settle down to a stationary regime, one always has to throw away a c
ertain number of iterates or periods while carrying out the numerical work. Howe
ver, how could one be confident that the transients have realy faded out?
In studies of critical phenomena and phase transition in physicall systems, it h
as been known that there exists so-called critical slowing down: it would take a
very long time for a system to reach e new equilibrium state, after having been
perturbed from an equilibrium state, if it had been very close to or was right
at the critical point. The same happens with the time evolution of nonlinear sys
tems, when they are close to a bifurcation point (see Hopf bifurcation).
A nice example of transient can be seen in the system of differential equations
discovered by Volta:
- x'=-x-5y-zy
- y'=-y-85x-xz
- z'=0.5z+xy+1
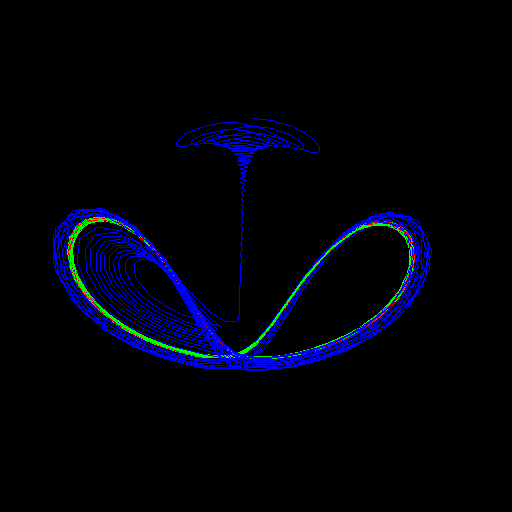
If one were not patient enough, the lower part of the figure could be mistaken as a Lorenz type attractor:
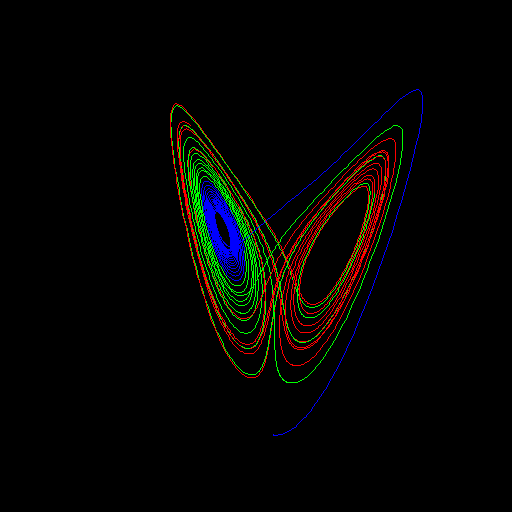
It is actually a fairly regular transient to a simple limit cycle.


