Stress States in a Beam
The following is from a project developed at Virginia Tech for
the ESM5984 Scientic Visualization and Multimedia Class.
Introduction to Glyphs
The problem of determining the principal stress state can be reduced to
an eigenvalue problem and visualized as a quadric surface. The
components of a second order stress tensor can be written in a more
familiar matrix format where it is easy to show that each matrix term is
a vector component acting on the differential element. Stress can be
represented as both a first order tensor or a second or tensor where the
stress vector is acting on a plane whos normal is ni. With the
condition ni=1, there will be four equations with four unknowns which
becomes an eigenvalue problem. The values on the diagonal are the three
eigenvalues (Principal Stresses) and the ni are the eigenvectors.
("orientations" of the Principal Stresses). When the differential
element is rotated into the principal stress state, the normal stresses
become maximum and minimum and the shear stresses go to zero. The
eigenvalues cam be determined by expanding the determinate into a
characteristic equation and solving for the roots. These roots or
eigenvalues, together with the principal direction, can be visualized as
a quadric surface (eliptical glyph) whose major and minor axis lengths
are the eigenvalues and the orientation of these axes is the
eigenvectors. Stress states will be represented as three dimensional
elliptical glyphs:
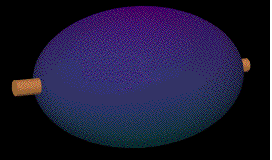
To enable easier viewing of the major and minor axis length as well as
the orientation of those axes, the glyph will have sections cut out,
showing the proper lengths of the axes.
Principal Stress States
Given a prismatic beam, subject to some arbitrary transverse loading, at
any point in the cross section, an element of material is subjected to
the normal stress and the shearing stresses. Consider the distribution
of the principal stresses in a narrow rectangular cantilever beam,
subjected to a concentrated load at its free end.
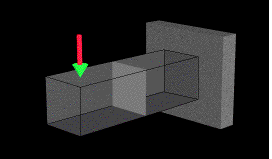View Stress States.
Brian S.
Amento , brian@discus.ise.vt.edu
Click image
to return to Class 1994 page.
