Greg Walker

Parametric Optimization of Experiments

Overview

Optimization can usually be accomplished with one of many gradient techniques that ensure quick and accurate convergence to a desired extremum of a particular objective function. These techniques are most reliable, however, when the function is "well-behaved". Gradient methods tend to fail when the objective function contains many local extrema. In this case, random search methods (such as genetic algorithms) can be used to locate a global extreme at the cost of requiring much longer computation times. An overwhelming advantage of these methods is their simplicity. For even more intricate objective function behavior, random search methods may not be able to determine the extrema reliably. It is suggested that more insight and reliability can be obtained through visualization of the objective function. Using this method should require a complete parametric evaluation of the function, but retains an encouraging element of simplicity. A parametric approach coupled with a visualization technique also allows the overwhelming advantage of being able to examine multiple criteria simultaneously.

Problem Description

Even though a visualization method can be applied to an enormous range of problems, this study will focus on a specific experimental optimization problem.

When new materials are invented the thermophysical properties of the material are usually unknown. For example, our research group is frequently interested in estimating the thermophysical properies of new composites that exhibit anisotropic behavior. To estimate the properties we must design an experiment that will give us the best results. A typical experimental optimization procedure is extremely complicated and usually is performed using a parametric approach, and only one criterion (for determining the "best" experiment) is used.

Ideally we want to make a temperature measurement in time at a single location on the unknown material. This temperature measurement is then used to extract (hopefully) the properties of thecomposite. A mathematical model of two dimensional conduction is used to calculate sensitivities of a calculated temperature to the thermophysical properties at a specific design point. If we visit a sufficiently large number of design points we can construct a parametric data set. For each design point we can generate a 3x3 symmetric sensitivity matrix (we have 3 thermophysical parameters in our problem). This matrix is then manipulated and visualized to show the optimum design point.

What are we looking for?

First we must invert the sensitivity matrix to give what we call the P-matrix. The oblique spheroid defined by this matrix represents the confidence region of the parameter estimates. At this point, we have two goals in mind:

1. To minimize the confidence region
2. To reduce correlation

There are several methods for minimizing the confidence region; some of which will be explored. The level of correlation should be reduced to ensure that we can estimate the parameters independently.

Minimization of the Confidence Region

• The e-criteria

  The confidence region should be minimized and one method for accomplishing this is to find the region where the confidence region has the smallest volume. Therefore, by locating the design whose determinant is smallest, we have effectively minimized the volume of the confidence region.

• The d-criteria

  Another method for minimizing the confidence region is to minimize the trace. Now the optimal experimental design will produce results whose confidence intervals are smallest. Note however, this may not be the location of smallest volume.

• The a-criteria

  In both previous paradigms, a single sensitivity might be large while the others are small. Looking at the determinant and/or the trace can give a "smoothed" result. If we are primarily interested in a single parameter we can examine the appropriate diagonal term independently of the rest. This experimental design will be optimal for estimating the parameter of interest.

Correlation

When there exists a linear dependence between any two parameters, they can not be estimated independently. We say the parameters are correlated. The level of correlation can be determined by scaling the P matrix using the simple formula Rij = Pij/(PiiPjj)^1/2. The diagonal terms become unity and the off-diagonal terms represent the degree of correlation. Experience tells us that if the an off-diagonal term is greater than 0.95 then the two parameters associated with that position in the matrix are correlated and can not be estimated independently. By visualizing where the maximum of-diagonal term is below the 0.95 threshold, we can determine if our optimal design case has uncorrelated parameters. We can then redesign the experiment (hopefully) so that we are close to the optimal sensitivity case and the parameters are uncorrelated.

Results

The e-criteria was examined to determine where the volume of the confidence region is smallest as a function of the design parameters.

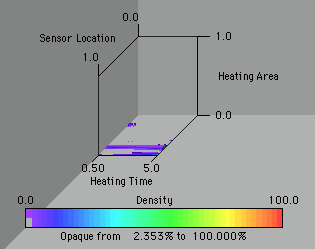
We see that there is not a large region that is more sensitive than most of the design space. Using this criteria in a gradient method might lead us to believe that we have a profoundly better design, when in fact it may not be. This also demonstrates that another design criteria might yield a wider choice of designs. The fact that the possible designs are so sparce indicates that we will probably have a hard time generating an adequate experiment to estimate the desired parameters accurately and independently. More analysis is needed before we make such a conclusion, however.

If we want to determine the level of correlation we can visulaize the maximum off-diagonal term in the R matrix. The values above 0.95 have been eliminated to give regions of "low-enough" correlation.

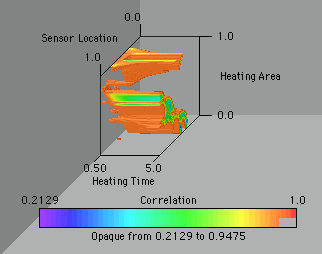
Something that has been impossible without this form of parametric study and visualization is to determine where the parameters are correlated. Historically the correlation is checked after a design is selected. If the parameters turn out to be correlated, the experimental design had to be re-thought. This picture shows us the regions where we can estimate parameters independently. Notice that the correlation is independent of heating time. This same result can be nearly obtained from the image of the maximum trace. This would suggest that a follow up analysis might not include heating time as an experimental parameter to be used to design a better experiment.

To demonstarte another approach to the problem, suppose that we are only interested in studying a single parameter after the exepriment. We can then examine the correlation of this parameter with the other two. Instead of visualizing the max off-diagonal term, we can look at the appropriate off-diagonal term.

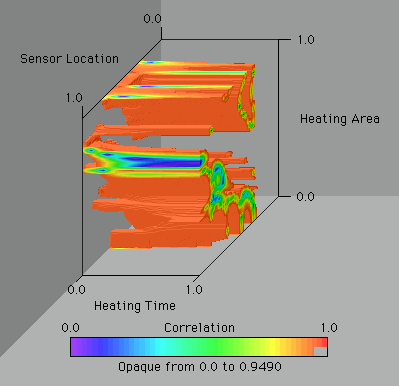
Since the images are similar we can assume that the parameter chosen in this case dominates the correlation of the whole system. Never the less, we can locate a design point that sufficiently uncorrelates the parameters.

Conclusions

With a combination of parametric study and visualization, the engineer has at his disposal a tool that proves to be infinitely more valuable than algorithms and routines. We can evaluate an experimental design using his intuition. The amount of information provided by visualizing several design criteria including correlation effects allows the designer to create experiments that should be much more adept at generating the appropriate information for parameter estimation.

Acknowledgements

• Dr. Ron Kriz - visualization
• Gordon Miller - presentation
• Joe Hanak and Debbie Moncman - previous work on this problem