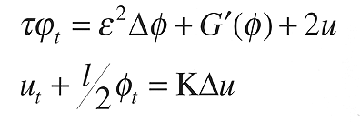
The phase field equations model the solidification of a pure material [Caginalp] [Fix] [Collins & Levine].
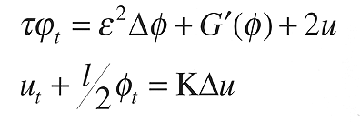
Here u(t,x) is the absolute temperature of the material and phi(t,x) is an order parameter which describes the phase of the material. Tau, epsilon, l and K are constants. G( phi) is a double well potential function with minima corresponding to the preferred phase; phi=1 represents solid whereas phi=-1 represents liquid. There exists an interval ( phi_1, phi_2 ) in which the problem is chaotic in nature. The double-well potential, G( phi), increases the complexity of this system of partial differential equations because of its non-convexnature. This model is, in part, the result of minimizing the total energy functional
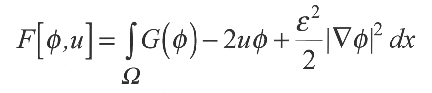
Numerical solutions of the Phase Field equations are obtained using a fortran program written by Dr. Matthias Heinkenschloss of the VPI&SU Mathematics Department. This program utilized Finite Elements Method to solve the system of equations. The numerical solutions obtained are based on the 2-Dimensional case where only the boundary of a square domain of pure material is thermally heated or cooled. Four physical situations are considered, each of which is defined by specific boundary conditions for u and phi. These initial conditions represent a solid interior heated at the boundaries, a liquid interior cooled at the boundaries, a solid quarter circle in liquid where the boundary temperature retains the initial temperature throughout and, lastly, a solid circular seed surrounded by liquid where the boundary temperature remains constant throughout. Each example is computed for 0.5 time units.
Visualization of numerical results show the evolution of the sharp phase interface and mushy temperature gradient. The use of PV WAVE allows one to observe the interaction of u and phi by viewing the contours of phi over the graph of u. The example given is the first initial condition.
G. Caginalp. An analysis of a phase field model of a free boundary. Archives of Rational Mechanics and Analysis, 92:205-245, 1986.
J.B. Collins and H. Levine. Diffuse interface model of diffusion-limited crystal growth. Physical Review B 31(9):6119-6122, 1985.
G.J. Fix. Phase field methods for the free boundary problems. In Free Boundary Problems: Theory and Application 2nd ed.. A Fusano and M. Primicerio eds. Pitman, Boston. pp. 580-589, 1983.