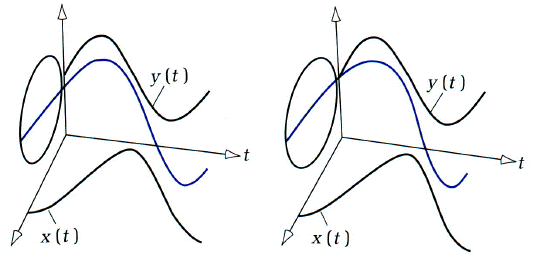
Now try to view the helix without the projections in the x-t and y-t planes in the figures shown below.
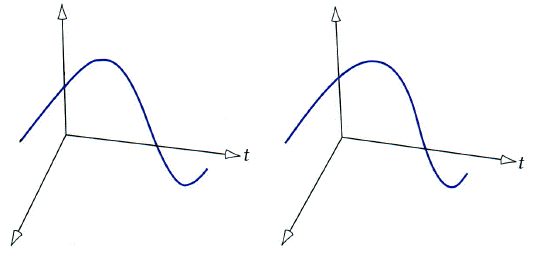
Two examples shown below are easily viewed without the add of special glasses. Stereographic visual tools can obviously add new dimensions to your data but is not always justified. Some excellent examples of applications where data can benefit from stereo are: 1. 3-D animation of chaos, 2. volume visualization of CT scans, and 3. synthesis of complex chemical structures by simulation-visualization (see Molecular Simulation Inc. software).
Stereo example shown below taken from reference: Computer Graphics, F.S. Hill, Jr., Macmillan Publishing Company, New York, 1990.

Now try to view the helix without the projections in the x-t and y-t planes in the figures shown below.

 Click
image to
return to Visualization home page.
Click
image to
return to Visualization home page.
R.D. Kriz
http://www.sv.vt.edu/classes/ESM4714/Gen_Prin/stereo/stereo.html
Va. Tech
College of Engineering
Revised 02/11/95